Also Fraktale sind relativ einfach zu verstehen. Der Fachidiot spricht bei Fraktalen von Selbstähnlichkeit. Das heißt, wenn ich an den Rand einer Mandelbrotmenge (benannt nach dem Franzosen Amerikaner Mandelbrot) heranzoome, finde ich nur noch mehr Apfelmännchen (Das sind die schwarzen Figuren, die man in dem anderen Beitrag sieht). Ursache dafür ist schon der mathematische Hintergrund, denn bei Fraktalen wird eine Gleichung immer wieder mit ihrem eigenen Ergebnis gefüttert. Aber ich erläutere das am besten mal am Beispiel…
Man nehme ein Blatt Papier und zeichne eine Strecke.
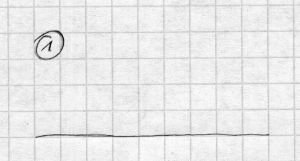
Diese Strecke unterteilt man in 3 gleich große Abschnitte.

Auf den mittleren Abschnitt setzt man ein gleichschenkliges Dreieck auf.
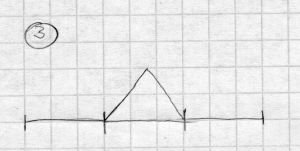
Und jetzt geht das Spiel eigentlich wieder von vorn los. Alle Strecken werden in 3 gleich große Abschnitte unterteilt …
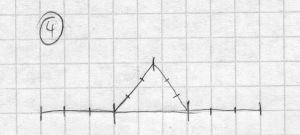
… es werden gleichschenklige Dreiecke aufgesetzt…

… und wieder werden die Strecken unterteilt.
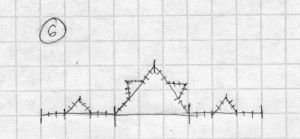
 usw. usf. Diese Wiederholungen nennt man Iterationen. Natürlich kann man endlos viele Iterationen durchlaufen lassen, aber ab einem bestimmten Punkt stellt man keinen Unterschied mehr fest, weil die Strecken so kurz geworden sind, dass sie mit bloßem Auge nicht mehr wahrzunehmen sind. Deswegen kann man bei Programmen eine sogenannte Iterationstiefe festlegen, welche die Anzahl der Wiederholungen festlegt.
usw. usf. Diese Wiederholungen nennt man Iterationen. Natürlich kann man endlos viele Iterationen durchlaufen lassen, aber ab einem bestimmten Punkt stellt man keinen Unterschied mehr fest, weil die Strecken so kurz geworden sind, dass sie mit bloßem Auge nicht mehr wahrzunehmen sind. Deswegen kann man bei Programmen eine sogenannte Iterationstiefe festlegen, welche die Anzahl der Wiederholungen festlegt.
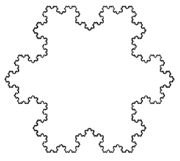
Hätte man oben begonnenes Experiment an mehreren Strecken fortgeführt, wäre diese Schneeflocke herausgekommen. Ich weiß, Fraktale sind ein kleines Universum für sich, aber ich hoffe, dass es jetzt ein bissel besser zu verstehen ist, was da vor sich geht.



